내쉬균형(Nash Equilibrium) 찾는 방법 합리적인 돼지게임 내시
내쉬균형(Nash Equilibrium)
서로 상대방의 전략에 대해 최선의 행동을 취하는 상태
-하지만 내시균형이 항상 최선의 이익을 가져다주는 것은 아님
1994년 노벨 경제학상을 수상한
수학자 존 포브스 내시(John Forbes Nash)가 만든용어로
내시균형이란
서로 상대방의 전략에 대해 최선의 행동을 취하는 상태입니다.
죄수의 딜레마에서의 내쉬균형은
'침묵'과 '자백'중에서 모두 '자백'하는 상태입니다.
(하지만 최선의 선택은 모두 '침묵'하는 상황이므로,
내시균형이 곧 최선의 이익을 나타내지는 않습니다)
게임의 구조가 정해지면
특정한 상태에 머물게 되고, 상대방의 전략에 대해
서로 최선의 행동을 취하고 있는 상태, 내시균형을 이룬다고 생각합니다.
만약, 내시균형이 아닌 상태가 발생되면,
누군가는 최선의 선택이 아닌 행동을 취하고 있는 것이어서
그러한 상태는 오래 지속되지 않습니다.
게임이론에서는 내시균형이 어디서 이뤄지는지 파악하는 것이 중요합니다.
(내시균형을 찾아야 다음에 일어날 상황도 어느정도 예측할 수 있기 때문)

합리적인 돼지게임(Rational Pigs)
'내시균형' 찾기 사례
합리적인 돼지게임(Rational Pigs)은
큰돼지와 작은돼지 두마리가 있다고 가정합니다.
우리의 왼쪽에는 손잡이가 있고, 우리의 오른쪽에는 먹이통이 있습니다.
돼지가 왼쪽으로 가서 손잡이를 올리게 되면, 오른쪽에 있는 먹이통에서
먹이가 쏟아지게 설계가 되어 있습니다.
작은 돼지는 더 빨리 뛸 수 있지만,
큰 돼지가 먹이통 앞에 오면 덩치에 밀려서 먹이를 먹을 수 없는 상황입니다.
두 돼지는 다음의 2가지 행동을 합니다.
-손잡이를 올린다
-먹이통 앞에서 기다린다
이러한 상황에서 합리적인 돼지게임(Rational Pigs)은
두 돼지가 어떤 행동을 취할지 관심을 가집니다.
합리적인 돼지 2X2표를 그려보면 다음과 같습니다.

①만약 작은돼지가 손잡이를 올리게 되면
큰돼지가 먹이통 앞에서 기다리게 됩니다.
큰돼지는 만족감이 커서 5라는 효용을 얻지만,
작은돼지는 만족감이 마이너스라서 -1이 됩니다.

①작은 돼지 : 손잡이 올리기 / 큰돼지 : 먹이통 앞에서 기다리기
-> 작은돼지 :-1 / 큰돼지 :5
작은돼지 입장에서 왼쪽의 손잡이를 올렸지만,
먹이를 먹을 수없어 효용이 마이너스입니다.
②큰 돼지가 손잡이를 올리고, 작은돼지가 먹이통 앞에서 기다리면
큰돼지가 먹이통에 올때까지 작은돼지가
먹이를 먹게 됩니다.
이러한 만족도는 작은돼지가 2, 큰돼지 만족도가 3이 될 것입니다.
②작은돼지 : 먹이통 앞에서 기다리기 / 큰돼지 :손잡이 올리기
-> 작은돼지 : 2/ 큰돼지 : 3

③작은돼지와 큰 돼지 둘 다 먹이통 앞에서 기다리면,
아무도 손잡이를 올리지 않아 먹이가 떨어지지 않게 됩니다.
이러한 경우 양 쪽 모두 만족도는 =0이 됩니다.
③작은돼지 & 큰돼지 모두 먹이통 앞에서 기다리기
-> 작은돼지 & 큰 돼지 : 0

④작은돼지와 큰 돼지 둘 다 손잡이를 올리게 되면,
작은돼지가 속도가 빨라 먹이를 먹을 수 있으나
곧 큰돼지가 와서 먹이를 다 먹어버리게 됩니다.
이 경우 작은돼지 만족도가 1, 큰돼지 만족도는 4입니다.
④작은돼지 & 큰 돼지 모두 손잡이 올리기
-> 작은돼지 1 / 큰돼지 4

내쉬균형(Nash Equilibrium) 찾는방법
상대방의 행동에 대응해 자신에게 이익이되는 숫자에 동그라미 쳐보기
합리적인돼지 게임의
4가지 상황에서 내시균형을 찾으려면
숫자에 동그라미를 그려 넣어보면 알 수 있습니다.
상대방의 행동에 대응해 자신에게 최대의 이익이 되는
숫자에 동그라미를 그리면 됩니다.
작은돼지 입장에서 생각
작은돼지 입장에서 큰 돼지가 손잡이를 올리면
작은돼지 입장에서 손잡이를 올리면 만족도 1,
먹이통 앞에서 기다리면 2의 만족도를 얻습니다.

1보다는 2의 만족도가 크기때문에 2에 동그라미를 칩니다.
(작은돼지 입장에서 큰돼지가 손잡이를 올리면 먹이통 앞에서 기다리는 것이 나은 행동)
한편, 작은돼지 입장에서 큰 돼지가 먹이통 앞에서 기다린다면,
손잡이를 올리면 만족도가 -1, 먹이통 아펭서 기다리면 만족도 =0입니다.

즉, 작은돼지 입장에서
큰돼지가 먹이통 앞에서 기다리면 같이
먹이통 앞에서 기다리는 편이 낫습니다.
즉, 작은돼지 입장에서 큰 돼지 행동과 상관없이
먹이통 앞에서 기다리는 것이 가장 최선의 행동입니다.
큰돼지 입장에서 생각
큰 돼지 입장에서 작은돼지가 손잡이를 올린다고 가정하면
손잡이를 올리면 만족도가 4,
먹이통 앞에서 기다리면 만족도가 5 입니다

-> 큰 돼지 입장에서 작은돼지가 손잡이를 올리는 행동에선
먹이통 앞에만족도가 더 높습니다.
큰 돼지 입장에서 작은돼지가 먹이통 앞에서 기다리고 있을 경우
손잡이를 올리면 만족도가 3, 먹이통 앞에서기다리면 만족도가 =0입니다.

-> 큰 돼지 입장에서 작은돼지가 먹이통 앞에서 기다리면
큰돼지는 그래도 손잡이를 올리는 것이 낫습니다.
위 4가지 사례를 모두 종합하여 동그라미를 나타내면
모두가 동그라미인,
작은돼지는 '먹이통 앞에서 기다리기'
큰돼지는 ' 손잡이 올리기'
가 가장 최선의 선택으로 내시균형을 이루게 됩니다.

즉, 게임이론에선 작은돼지가 먹이통 앞에서 기다리고,
큰 돼지가 손잡이를 올리는 조합이 가장 많이 일어날 가능성이 높습니다.
내쉬균형이 무조건
일어나지 않을 수 있음
-그럴땐 게임이론을 지배하는 게임구조를 변경해보는 것은 어떨까?
-새로운 보상제도를 만들거나 벌칙을 강화하거나?
위 게임과 마찬가지로 경찰과 도둑 게임에서는
내쉬균형이 성립하지 않습니다.
①경찰 : 순찰을 돈다, 도둑 : 빈집을 턴다
-> 경찰 만족도 1, 도둑 -1
②경찰 : 순찰은 돈다, 도둑 : 빈집 털지 않는다
-> 경찰 만족도 -1, 도둑 0
③경찰 : 순찰을 돌지 않는다, 도둑 : 빈집을 턴다
-> 경찰 만족도 -1, 도둑 1
④경찰 : 순찰을 돌지 않는다, 도둑 : 빈집을 털지 않는다
-> 둘다 만족도 =0
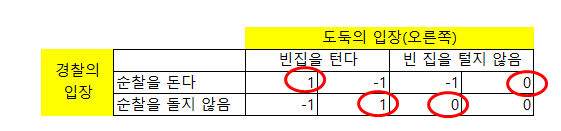
따라서 경찰과 도둑의 행동은 일정한 형태로 정해지지 않게 됩니다.
경찰이 순찰을 돌고 있다는 정보를 입수한 도둑은 범행을 저지르지 않고,
경찰은 순찰을 돌지 않아도 별일 없을 것이라는 생각이 들게 되어
순찰을 잘 돌지 않는 게으름을 핍니다.
이후 경찰이 순찰이 돌지 않는날이 지속되면 도둑은 빈집을 털러 갑니다.
이러한 사실을 알게되면 경찰은 다시 순찰을 재개합니다.
즉, 내시균형이 성립하지 않는 구조이며,
이러한 다람쥐 쳇바퀴 도는 상황이 계속 반복되게 됩니다.
따라서 내시균형이 존재하지 않으면
게임이론을 지배하는 규칙을 변경하여 게임의 구조를 바꾸는 것도 방법입니다.
경찰이 순찰을 돌지 않아 도둑이 빈집을 털면
경찰은 -1의 이익을 얻지만, 도둑은 1입니다.
만약, 경찰에게 돌아가는 불이익(벌금 500만원)을 무겁게 한다면
경찰은 열심히 순찰을 돌게 되지만,
과도한 벌금으로 경찰의 지원자가 줄어들 수 있습니다.
이러한 경우 빈대를 잡으려다가 초가삼간 태우는 상황이 올 수 있으므로
반대로 순찰행위에 대해 보수를 지급하는 경우도 생각해볼 수 있습니다
기존 게임 구조 : 경찰이 헛수고 한 만큼 -1 이익
-> 새로운 게임구조 : 하루에 100만원 보수 지급 +1 이익으로 변경

도둑이 빈집을 털든 말든,
경찰은 매일 순찰을 돌게 될 것이며, 도둑을 잡게되면 특별보너스까지 지급한다면
강력한 동기부여 수단이 될 수 있습니다.
즉, 벌칙을 강화하거나 새로운 보상제도를 만들어서
게임구조를 변경하는 것도 하나의 방법이 될 수 있습니다.
문제가 발생하면, 문제가 일어난 게임 구조를 이해하고
원인을 제거해나가고, 풀리지 않는다면 게임 규칙을 변경하는 방법을
강구해보면 좋을 것 같습니다.
이상, 내시균형 및 합리적인돼지게임에 대해 알아보았습니다.
자료 : 게임이론의 사고법 참고
위 내용은 별별의 개인적인 분석이므로 참고용으로만 봐주시면 감사하겠습니다:)
이웃추가, 공감도 부탁드립니다

